问题

问题1

问题：给出一个可数集的例子：它是有界的，但是没有最小值。

解答：令$x_n = \frac{1}{n}$，这里$n \in \mathbb{N}_0$，也就是正整数。

视频：B站；头条号；知乎；百家号；快手。

问题2

问题：给出一个可数集$A$的例子：它是有界的，并且它严格包含于它的极限点组成的集合$B$之中（或者说$A$是它的极限点组成的集合$B$的真子集）。

解答：考虑集合$(0,1)$中的所有有理数，即：$A = \{x | 0 < x < 1, x\text{为有理数}\}$，此时$B = \{x | x \le x \le 1\}$。

视频：B站；头条号；知乎；百家号；快手。

问题3

问题：给出一个可数集$A$的例子：它有一个极限点既不等于$A$的上确界，也不等于$A$的下确界。

解答：考虑序列$x_n = 1 + (-1)^n\frac{1}{n}$,这里$n \in \mathbb{N}_0$为非负整数。此时极限点为$1$，上确界为$\frac{3}{2}$，下确界为$0$。

视频：B站；头条号；知乎；百家号；快手。

问题4

问题：讨论下列序列的上界的存在性：\[x_n = \frac{n^2+1}{n+1}, \quad n \in \mathbb{N}.\]

解答：不存在。

直观方法

当$n$足够大的时候，$n^2+1$可以由$n^2$逼近，而$n+1$由$n$逼近，因此$\frac{n^2+1}{n+1}$能被$\frac{n^2}{n}$逼近，也即是$n$，因此，对于足够大的$n$，序列$x_n$和$n$是一致的，因此是无界的。

正式方法

$x_n = \frac{n^2+1}{n+1} = \frac{n^2-1+2}{n+1} = \frac{(n+1)(n-1)+2}{n+1}=(n-1)+\frac{2}{n+1}$

由于$\frac{2}{n+1} > 0$对所有自然数$n \in \mathbb{N}$成立，我们有$n-1+\frac{2}{n+1}$是大于$n-1$。因为序列$n-1$是无界的，因此序列$x_n = n-1+\frac{2}{n+1}$也是无界的。

另一个正式方法

假设给定的序列存在一个上界$L$，于是

\[\begin{aligned}x_n \le L \\ \frac{n^2+1}{n+1} \le L \\ n^2+1 \le L(n+1) \\n^2-Ln + 1 – L \le 0\end{aligned}\]

最后一个关于$n$的二次多项式的不等式，仅仅对于某个区间$(n_1,n_2)$内的自然数$n$成立，因此它只能对有限个自然数成立。这就和我们的假设（不等式$x_n \le L$对于所有的$n \in \mathbb{N}$成立）矛盾。更确切地说，如果用$\Delta$表示不等式左边地多项式的判别式，那么有

• 如果$\Delta < 0$，那么不等式不成立。
• 如果$\Delta = 0$，左边的多项式有两个相等的无理根，因而在$\mathbb{N}$中没有根。
• 如果$\Delta > 0$，那么不等式的解为 \[ \frac{L – \sqrt{\Delta}}{2} \le n \le \frac{L + \sqrt{\Delta}}{2}, \] 因此，不等式最多对有限个自然数成立。

视频：B站；头条号；知乎；百家号；快手。

问题5

问题：找到下列序列的上确界： \[x_n = \frac{2n+1}{n+3}, \quad n \in \mathbb{N}.\]

解答：$\sup{x_n}=2$.

直观方法

\[x_n = \frac{2n+1}{n+3} = \frac{(2n+6) – 5}{n+3} = 2- \frac{5}{n+3}\] 由于比值$\frac{5}{n+1}$是正的，并且随着$n$的增大可以任意小，因而序列的上确界是2。因此，所有的$x_n$严格小于2，并且如我们所愿趋向于2.

严格使用定义的正规方法（为了使用这个方法，需要事先知道或者猜出上确界的值）

如果我们猜上确界是2，我们必须验证：

A) 对所有$n \in \mathbb{N}$有$\frac{2n+1}{n+3} \le 2$（即2是上界）；

B) 对任意的$\epsilon > 0$，存在$n \in \mathbb{N}$满足$\frac{2n+1}{n+3} > 2 – \epsilon$（即2是最小上界）。

A)的证明： \[\begin{aligned}\frac{2n+1}{n+3} \le 2\\ 2n+1 \le 2n+6\end{aligned}\]

B)的证明： \[\begin{aligned}\frac{2n+1}{n+3} > 2 – \epsilon \\ 2n+1 > (2-\epsilon)(n+3) \\ \epsilon{n} > 5 – 3\epsilon \\ n>\left(\frac{5 – 3\epsilon}{\epsilon}\right)\text{的整数部分}\end{aligned}\]

于是，给定$\epsilon$，存在无穷多个数满足给定的不等式，第一个满足条件的自然数是 \[ n_{\min} = \left(\frac{5-3\epsilon}{\epsilon}\right)\text{的整数部分} + 1 \]

最小上界的搜索方法（使用这个方法，事先不需要知道或者猜出上确界的值）

如果存在上界$L$，那么有 \[\begin{aligned}x_n = \frac{2n+1}{n+3} \le L\\ (2-L)n \le 3L – 1\end{aligned}\]

情形1 $L > 2$

\[\begin{aligned}(2-L)n \le 3L – 1 \\ n \ge \frac{3L – 1}{2-L}\end{aligned}\]

当$L > 2$时，比值$\frac{3L-1}{2-L}$是负的，所以最后的不等式对所有的$n \in \mathbb{N}$成立。

情形2 $L < 2$

\[\begin{aligned}(2-L)n \le 3L – 1 \\ n \le \frac{3L-1}{2-L}\end{aligned}\]

自然数集是没有上界的，最后的等式并不是对所有自然数成立，而仅仅对这样一些自然数成立： \[ n \le \left(\frac{3L-1}{2-L}\right)\text{的整数部分} \]

情形3 $L=2$

令$L=2$，原来的不等式 \[ (2-L)n \le (3L-1) \] 变为$0 \le 5$，显然对所有$n \in \mathbb{N}$成立。

结论： 所有的上界的集合是所有的大于等于2的实数组成的集合，因此，上确界是2。

视频：B站；头条号；知乎；百家号；快手。

问题6

问题：使用定义说明下列序列的下确界是否等于2： \[ x_n = \frac{3n+1}{n}, \in \mathbb{N}_0. \]

解答：我们必须验证：

A) 对所有$n \in \mathbb{N}_0$有$\frac{3n+1}{n} \ge 2$（即2是下界）；

B) 对任意的$\epsilon > 0$，存在$n \in \mathbb{N}_0$满足$\frac{3n+1}{n} < 2 + \epsilon$（即2是最大下界）。

A)的证明：

\[\begin{aligned}\frac{3n+1}{n} \ge 2 \\ 3n+1 \ge 2n \\ n \ge -1\end{aligned}\]

对所有的$n \in \mathbb{N}_0$成立的

B)的证明：

\[\begin{aligned}\frac{3n+1}{n} < 2 + \epsilon \\ 3n+1 < (2 + \epsilon)n \\ n(1 – \epsilon) < -1 \\ n(\epsilon-1) > 1\end{aligned}\]

现在我们有两种情况：

情形1 $\epsilon > 1$

\[\begin{aligned}n(\epsilon-1) > 1 \\ n > \frac{1}{\epsilon-1}\end{aligned}\]

因此，如果$\epsilon > 1$, 只要选择一个大于$\frac{1}{\epsilon-1}$的整数部分的自然数$n$即可。

情形2 $\epsilon \le 1$

$n(\epsilon-1) > 1$对于$n \in \mathbb{N}_0$永远不会成立，因为$n > 0$而$(\epsilon-1) \le 0$ 因此，如果$\epsilon \le 1$，不存在自然数满足$\frac{3n+1}{n} < 2 + \epsilon$.

结论：2不是下确界。

视频：B站；头条号；知乎；百家号；快手。

问题7

问题：找到下列序列的上确界和下确界： \[ x_n = \frac{n-1}{n^2+1}, \in \mathbb{N}. \]

解答：$\sup_{n \in \mathbb{N}}{\{x_n\}} = \frac{1}{5}$; $\inf_{n \in \mathbb{N}}{\{x_n\}} = -1$.

直观方法

我们通过计算出一些项来观察序列的性质。

序列从$x_0$到$x_2=x_3$是递增的，从$x_3$开始是递减的，因而$x_2=\frac{1}{5}$是最大值，而$x_0=-1$是最小值。实际上$x_0=-1$是序列中唯一的负数项，它对应于$n=0$时的唯一的负分子$-1$。

递增或递减项的研究

我们来寻找$n \in \mathbb{N}$使得序列时递增的。也就是 $x_n \le x_{n+1}$

\[\begin{aligned}\frac{n-1}{n^2+1} \le \frac{(n+1)-1}{(n+1)^2+1} \\ (n-1)[(n+1)^2+1] \le n(n^2+1) \\ n^2-n-2\le 0 \\ -1 \le n \le 2\end{aligned}\]

因此

\[ x_0 \le x_{0+1} = x_1 \le x_{1+1} = x_2 \le x_{2+1} = x_3. \]

类似的，当$n > 2$时$x_n > x_{n+1}$，于是

\[ x_3 > x_{3+1}=x_4 > x_{4+1}=x_5 > x_6 > x_7 > \cdots \]

总的来说，序列在前四项是递增的，从第五项开始是递减的。

结论： 最小值是$-1$而最大值是$\frac{1}{5}$。

视频：B站；头条号；知乎；百家号；快手。

问题8

问题：找到下列序列的上确界和下确界：

\[ x_n = \left\{ \begin{aligned} &\frac{n}{4-n^2}, &&\quad n \in \mathbb{N}, n \neq 2,\\ &1, &&\quad n=2 \end{aligned} \right. \]

解答：$\sup_{n \in \mathbb{N}}{\{x_n\}} = 1$; $\inf_{n \in \mathbb{N}}{\{x_n\}} = -\frac{3}{5}$.

直观方法

我们通过计算出一些项来猜测序列的性质：序列到$x_2$是递增的，从$x_2$到$x_3$是递减的，从$x_3$开始又是递增的，保持为负数。因此，很明显，最大值等于1而最小值等于$-\frac{3}{5}$。

递增项或递减项的研究

我们来研究$n \ge 3$的序列，来寻找对于哪些值$n$它是递增的。也就是：$x_n \le x_{n+1}$

\[\begin{aligned}\frac{n}{4-n^2} \le \frac{n+1}{4-(n+1)^2} \\ n[4-(n+1)^2] \le (n+1)(4-n^2) \\ n^2 + n + 4 \ge 0\end{aligned}\]

对于所有$n \in \mathbb{N}$成立。 因此，序列在$n \ge 3$时是递增的，有下列的性质：

\[\begin{aligned} &x_0=0;x_1=\frac{1}{3};x_2=1\\ &-\frac{3}{5}=x_3 \le x_4 \le x_5 \le \cdots \le x_n \le \cdots \le 0 \end{aligned}\]

结论：我们有结论：最大值等于1而最小值等于$-\frac{3}{5}$

视频：B站；头条号；知乎；百家号；快手。

问题9

问题：找到下列使用递归公式定义的序列的下确界和上确界（如果存在的）：

\[ \left\{ \begin{aligned} &a_{n+1} = \sqrt{a_n},\\ &a_0 > 0. \end{aligned} \right. \]

解答：如果$a_0 \le 1$，那么$\inf_{n}{\{a_n\}} = a_0$，$\sup_{n}{\{a_n\}} = 1$。 如果$a_0 \ge 1$，那么$\inf_{n}{\{a_n\}} = 1$，$\sup_{n}{\{a_n\}} = a_0$。

事实上，通过计算开始的一些项，我们有

\[ \begin{aligned} &a_0,\\ &a_1 = \sqrt{a_0} = a_0^{\frac{1}{2}},\\ &a_2 = \sqrt{a_1} = \sqrt{\sqrt{a_0}} = a_0^{\frac{1}{4}},\\ &a_3 = \sqrt{a_2} = \sqrt{\sqrt{\sqrt{a_0}}} = a_0^{\frac{1}{8}},\\ &\text{etc.} \end{aligned} \]

很明显，递归定义的序列实际上可以写成：

\[ a_n = a_0^{\frac{1}{2^n}}. \]

情形1 $0 < a_0 < 1$.

我们来研究序列的性质：

\[\begin{aligned}n_1 \le n_2 \\ 2^{n_1} \le 2^{n_2} \\ \frac{1}{2^{n_1}} \ge \frac{1}{2^{n_2}} \\ a_0^{\frac{1}{2^{n_1}}} \le a_0^{\frac{1}{2^{n_2}}} \\a_{n_1} \le a_{n_2}\end{aligned}\]

总结起来就是：

\[ n_1 \le n_2 \Leftrightarrow a_{n_1} \le a_{n_2} \]

这意味着序列是递增的。因此序列的第一项就是最小值，上确界，通过观察下面的函数$y=a_0^x$的图像，可以发现$0 \le a_n \le 1$以及$a_n$随着$n$的增大越来越靠近1，也就是$1 = \sup\{a_n\}$，换句话说 \[ \lim_{n \to \infty}{a_0^{\frac{1}{2^n}}} = 1. \]

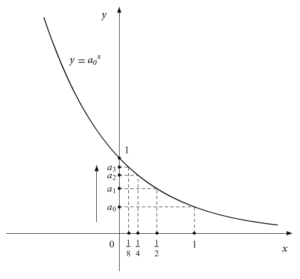
情形2 $a_0 > 1$ 类似。

视频：B站；头条号；知乎；百家号；快手。

问题10

问题：如图所示，回答下列问题：

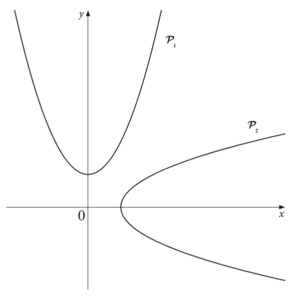
(a) 抛物线$P_1$是某个函数的图像吗？
(b) 抛物线$P_2$是某个函数的图像吗？

解答：(a)不是 P1的图像不可能是变量$x$的函数的图像，因为有一些平行于$y$轴的直线与P1相交于两个点$P_1$和$P_2$。 (b)是 每一条平行于$y$轴的直线和P2只相交于一个点，因而满足函数的定义。

视频：B站；头条号；知乎；百家号；快手。

问题11

问题：下面哪些函数和函数$y=x$是相等的？

(1) $y = \sqrt{x^2}$
(2) $y = \sqrt[3]{x^3}$
(3) $y = (\sqrt{x})^2$
(4) $y = (\sqrt{|x|})^2$
(5) $y = \log_{e}{e^x}$
(6) $y = e^{\log_{e}{x}}$

解答：（2）和（5）

视频：B站；头条号；知乎；百家号；快手。

问题12

问题：考虑下面的函数，哪些函数是一致的，哪些函数是其中一个函数是另一个函数的限制或延拓：

(1) $y = x$
(2) $y = \sqrt{x^2}$
(3) $y = \sqrt[3]{x^3}$
(4) $y = (\sqrt{x})^2$
(5) $y = (\sqrt{|x|})^2$

解答：(4)是(1)和(3)的限制，也是(2)和(5)的限制，反过来，(1)和(3)是(4)的延拓（扩展），(2)和(5)也是(4)的延拓。

视频：B站；头条号；知乎；百家号；快手。

问题13

问题：举一个函数例子$y=f(x)$，使得函数$y = \frac{1}{f(x)}$是给定函数的一个严格限制，也就是$\frac{1}{f(x)}$的图像是严格包含于$y=f(x)$图像中。

解答：考虑如下函数：

\[ f(x) = \left\{ \begin{aligned} &0, \quad 1 < x < 3,\\ &1, \quad x \le 1 \text{ or } x \ge 3 \end{aligned} \right. \]

此时

\[ \frac{1}{f(x)} = \left\{ \begin{aligned} &\text{not defined}, \quad 1 < x < 3,\\ &1, \quad x \le 1 \text{ or } x \ge 3 \end{aligned} \right. \]

视频：B站；头条号；知乎；百家号；快手。

问题14

问题：考虑定义在整个实数轴$\mathbb{R}$上的函数$y=x^2+1$，如图，有多少组函数$f_1(x)$和$f_2(x)$（它们的定义域分别为$D_1$和$D_2$）满足如下条件：

（1）$f_1$和$f_2$都是$f$的限制；
（2）$f_1$和$f_2$都是单射；
（3）$D_1 \cup D_2 = \mathbb{R}$。

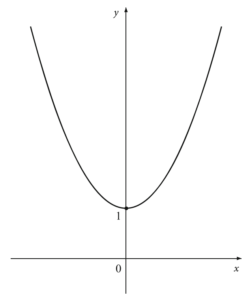
解答：无穷多个，实际上，最自然的一对函数如下：

\[ \left\{ \begin{aligned} &f_1(x)=x^2+1,\\ &x < 0. \end{aligned} \right. \quad \left\{ \begin{aligned} &f_2(x)=x^2+1,\\ &x \ge 0. \end{aligned} \right. \]

或者

\[ \left\{ \begin{aligned} &f_1(x)=x^2+1,\\ &x \le 0. \end{aligned} \right. \quad \left\{ \begin{aligned} &f_2(x)=x^2+1,\\ &x > 0. \end{aligned} \right. \]

我们还可以定义无穷多个其他的函数.例如

\[ \begin{aligned} &f_1(x) = x^2+1, \quad x <-1, \text{ or } -1 < x < 0, \text{ or } x = 1,\\ &f_2(x) = x^2+1, \quad x =-1, \text{ or } 0 \le x < 1, \text{ or } x > 1,\\ \end{aligned} \]

把它推广，可以这样定义：对任意$n \in \mathbb{N}$,

\[ \begin{aligned} &f_1(x) = x^2+1, \quad x <-n, \text{ or } -n < x < 0, \text{ or } x = n,\\ &f_2(x) = x^2+1, \quad x =-n, \text{ or } 0 \le x < n, \text{ or } x > n,\\ \end{aligned} \]

再次推广，我们可以这样的函数对，只要它们的定义域$D_1$和$D_2$满足如下条件即可：

\[ \left\{ \begin{aligned} &D_1 \neq \emptyset,\\ &D_2 \neq \emptyset,\\ &D_1 \cap D_2 = \emptyset,\\ &D_1 \cup D_2 = \mathbb{R},\\ &(x \in D_1, x \neq 0) \Leftrightarrow -x \in D_2. \end{aligned} \right. \]

注意到这样的关于$\mathbb{R}$划分$\{D_1,D_2\}$有无穷多。

视频：B站；头条号；知乎；百家号；快手。

问题15

问题：注意到如果函数$g$的定义域是关于原点对称的（也就是，$x \in D(g)$当且仅当$-x\in D(g)$），那么称$g$是偶函数，如果对所有的$x \in D(g)$有$g(x) = g(-x)$，称$g$是奇函数，如果对于所有的$x \in D(g)$有$g(x) = -g(-x)$。 众所周知，任意的函数$f$能够表示为一个偶函数$f_E$和一个奇函数$f_O$的和。例如

\[ \begin{aligned} f_E(x) = \frac{f(x) + f(-x)}{2},\\ F_O(x) = \frac{f(x) – f(-x)}{2}. \end{aligned} \]

是否存在另一组像上面一样的函数$f_E$和$f_O$。

解答：没有了，如果$\varphi$是偶函数，$\psi$是奇函数，满足 \[ f(x) = \varphi(x) + \psi(x), \] 那么 \[ f(-x) = \varphi(-x) + \psi(-x) = \varphi(x) – \psi(x), \] 因此 \[ \frac{f(x) + f(-x)}{2} = \varphi(x), \] 和\[ \frac{f(x) – f(-x)}{2} = \psi(x). \]

视频：B站；头条号；知乎；百家号；快手。

问题16

问题：定义在整个实数轴$\mathbb{R}$上的函数$f$称为是周期的，如果存在实数$p > 0$，使得对于所有的$x \in \mathbb{R}$都有$f(x+p)=f(x)$（例如$y = \sin{x}$）。下面结论是否成立：如果非常数函数$f$是一个周期函数，那么它的周期$p$的集合有一个最小值？

解答：否，不成立，考虑如下函数： \[ f(x)=\left\{ \begin{aligned} &1, \quad\text{$x$为有理数}\\ &0, \quad\text{$x$为无理数} \end{aligned} \right. \] 设$r$为一个给定的有理数，我们有

• 如果$x$是有理数，那么$x+r$是有理数，于是$f(x+r)=f(x)=1$;
• 如果$x$是无理数，那么$x+r$是无理数，于是$f(x+r)=f(x)=0$.

于是对于所有$x \in \mathbb{R}$，都有$f(x+r)=f(x)$，很明显，集合$\{r \in \mathbb{Q} : r>0\}$没有最小值。

视频：B站；头条号；知乎；百家号；快手。